第二章 信息的表示和处理
- 无符号编码 基于传统的二进制表示法,表示大于或者等于零的数字
- 补码编码 表示有符号整数最常见的方式
- 浮点数编码 表示实数的科学计数法的以2为基数的版本
信息存储
大多数计算机使用 8位 (1byte) 作为最小的可寻址的内存地址
机器级程序将内存视为一个非常大的字节数组,称为 虚拟内存
内存的每个字节有唯一标识,称为 地址,所有可能地址的集合称位 虚拟地址空间
每个程序对象可简单的视为一个字节块,而程序本身就是一个字节序列
十六进制
二进制与十六进制
当值是 2的非负整数 n次幂时,即 x = 2^,当 n = i + j * 4 的时候,0 <= i <= 3,第一位是 2 ^ i 例如 2048 = 2 ^11, n = 3 + 2 * 4,则 2048D = 800H
十进制与十六进制
同上例,800H = 8 * 16 ^ 2 + 0 * 16 ^ 1 + 0 * 16 ^ 0
字数据大小
字长 指明指针数据的标称大小,虚拟地址是以这样的一个字来编码的
字长决定的最重要的系统参数就是虚拟地址空间的最大大小
对于字长为 ω 位的程序而言,虚拟地址的范围为 0 ~ 2 ^ ω - 1,程序最多访问 2 ^ ω 个字节
字节顺序
最低有效字节在前面的方式,称为小端法 (Android, iOS) 最高有效字节在前面的方式,称为大端法
近代大多数处理器使用双端法
C语言 表示字符串
C语言中的祖父穿被编码为一个以 null (值为0) 字符结尾的字符数组
异或^ 的有趣用法 练习2.10
void swap(int *x, int *y) {
*y = *x ^ *y; // a | a ^ b
*x = *x ^ *y; // a ^ a ^ b | a ^ b
*y = *x ^ *y; // a ^ a ^ b | a ^ a ^ b ^ a ^ b
}
// 上述代码交换了 x 与 y 指向的地址
// 因为 a ^ a = 0
掩码
位运算的常见用法是实现掩码运算 掩码是一个位模式,表示从一个字中选出的位集合 表达式 ~0 将生成一个全 1的掩码 例: 掩码 0xFF 表示一个字的低 8位,位级运算 0x89ABCDEF & 0xFF 将得到 0x000000EF.
位移运算
当移动一个 x 位的值时,移位指令只考虑位移量的低 log2(x) 位
因此实际的位移量就是通过计算 k mod x 得到的
int x = 0xFEDCBA98 << 32; // 左移 0
int y = 0xFEDCBA98 << 36; // 左移 4
int z = 0xFEDCBA98 << 40; // 左移 8
左移
在低位补 0,高位丢弃
右移
逻辑右移
高位补 0,低位丢弃
算术右移
高位补符号位,低位丢弃
整数表示

无符号数的编码
一个 x 位的二进制数,最多表示 2 ^ x - 1的十进制
补码编码
最高有效位也称为符号位 符号位为 1 时,表示值为负 符号位为 0 时,表示值为正
ω 位补码所能表示的值得范围
Tmin = -2 ^ (w - 1)
Tmax = 2 ^ (w - 1) - 1
注:
- 设置最高位为负权,其他位清除 和 设置最高位为正,清除其他位
二者的值是相同的,因此补码表示正数的范围比负数小 1
|Tmin| = |Tmax| + 1 - 最大无符号数值刚好比补码的最大值的两倍大一点
UMax_w = 2TMax_w + 1 - 反码加一”只是补码所具有的一个性质,不能被定义成补码。负数的补码,是能够和其相反数相加通过溢出从而使计算机内计算结果变为0的二进制码。这是补码设计的初衷,具体目标就是让1+(-1)=0,这利用原码是无法得到的。
有符号数与无符号数之间的转换
保持位值不变,只是改变了解释这些位的方式
例:-12345 = 53191
可以发现 12345 + 53191 = 65536 = 2 ^ 16

拓展一个数字的伟表示
无符号数的零拓展
将无符号数转换为一个更大的数据类型,我们只要简单地在表示的开头添加 0,这种运算被称为 零拓展
补码数的符号拓展
将一个补码数字转换为一个更大的数据类型,可以执行一个 符号拓展,在表示中添加最高有效位的值
例:-12345 的补码 和 53191 的无符号表示在 16 位字长时是相同的,但是在 32 位字长时确实不同的。 -12345 得 十六进制表示为 0xFFFFCFC7,而 53191 的十六进制表示为 0x0000CFC7 前者使用的是符号拓展 —— 开头添加了 16 位的 1 后者使用了零拓展 —— 开头添加了 16 位的 0
101表示 -3,使用符号拓展之后 1101 也表示 -3 相似的 111 和 1111 表示的都是 -1
整数加法
无符号加法
溢出情况:1110 + 0010 = 10000,14 + 2 = 16 丢弃最高位后,得到 0000,和 16 mod 16 = 0 一致
补码加法
给定在 -2^(w-1) ~ 2^(w-1)-1 之内的整数 x 和 y,它们的和就在范围 -2^w ~ 2^w-2 之间
当结果超过 2^(w-1)-1 时,截断的结果会减去 2^w,这种情况称为 正溢出
当结果小于 -2^(w-1) 时,截断的结果会加上 2^w,这种情况称为 负溢出

无符号乘法

补码乘法

乘以常数
在大多数机器上,整数乘法指令相当慢,需要 10 个或更多, i7 Haswell 3个 因此,编译器使用了一项重要的优化,试着用位移和加法运算的组合来代替乘以常数因子的乘法
乘以2的幂
 例:11D = 1011B,11 * 4 = 11 * 2 ^ 2
此时k = 2,因此 1011 << 2,得101100 = 44D
例:11D = 1011B,11 * 4 = 11 * 2 ^ 2
此时k = 2,因此 1011 << 2,得101100 = 44D
因此,左移一个数值,等价于执行一个与 2 的幂相乘的无符号乘法 注:溢出时,通过位移得到的结果也是一样的,101100 截断后是 1100,12 = 44 mod 16
常数
例:x * 14,因为14 = 2^3 + 2^2 + 2^1 因此编译器将乘法重写为 (x << 3) + (x << 2) + (x << 1),或更好的 (x << 4) - (x << 1)
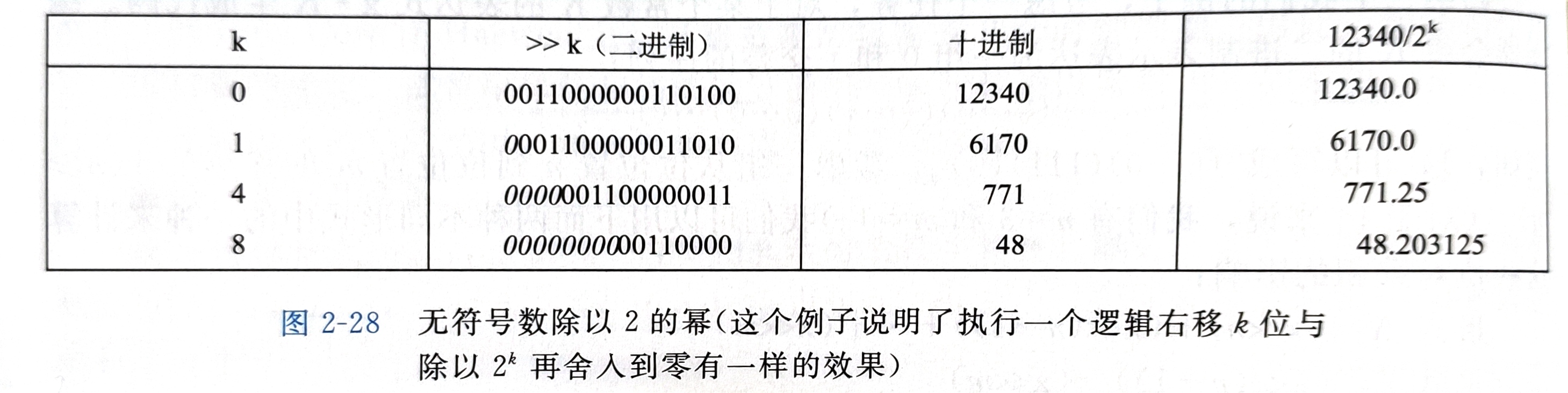
除以2的幂
整数除法比整数乘法更慢,需要 30 个或更多的时钟周期
通过 右移 来实现除以2的幂
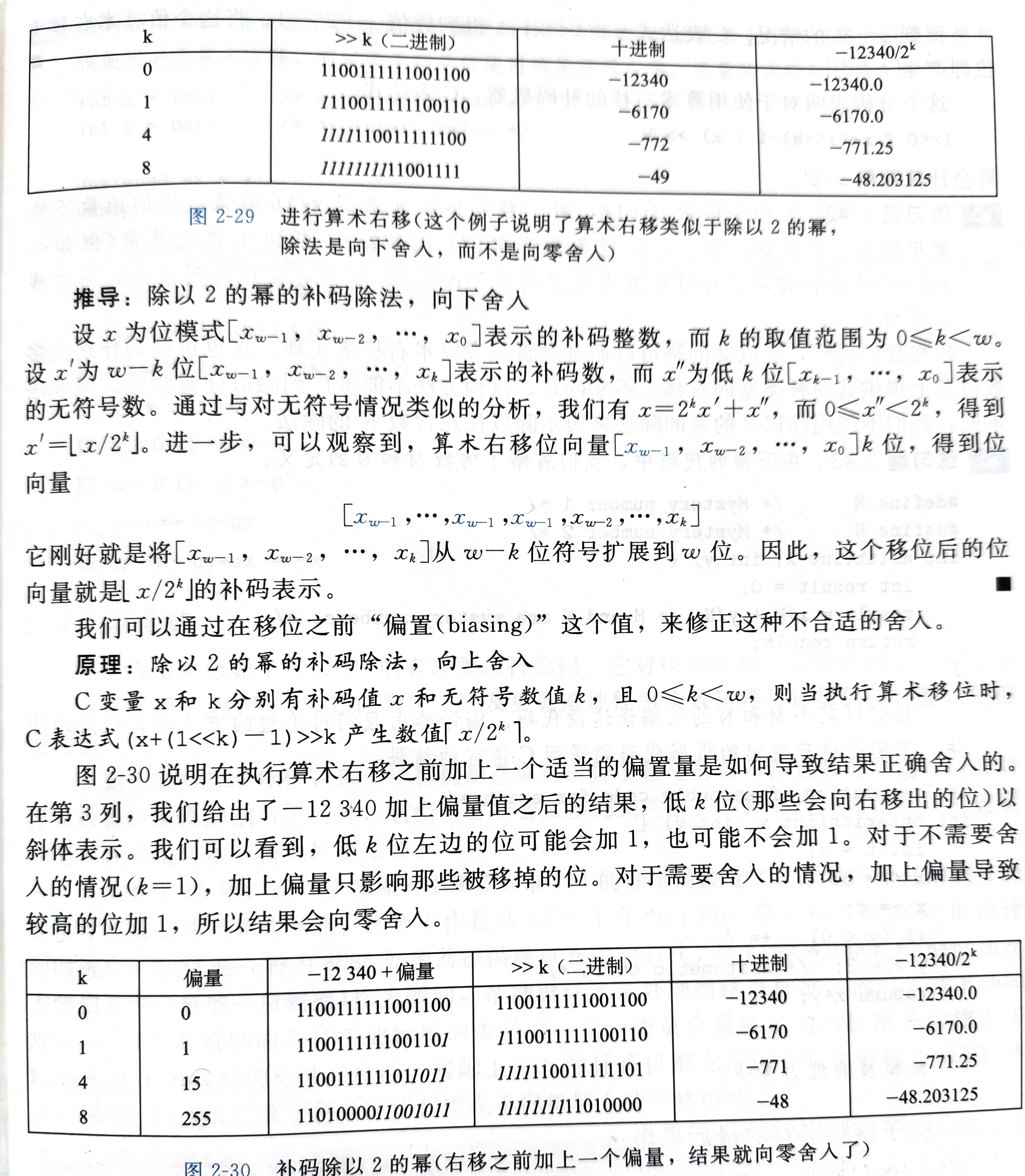
逻辑右移和算术右移,区分无符号数和补码数
如遇小数,向下取整
 注:这种方法无法推广到除以任意常数
注:这种方法无法推广到除以任意常数
浮点数
浮点数标准 IEEE 754
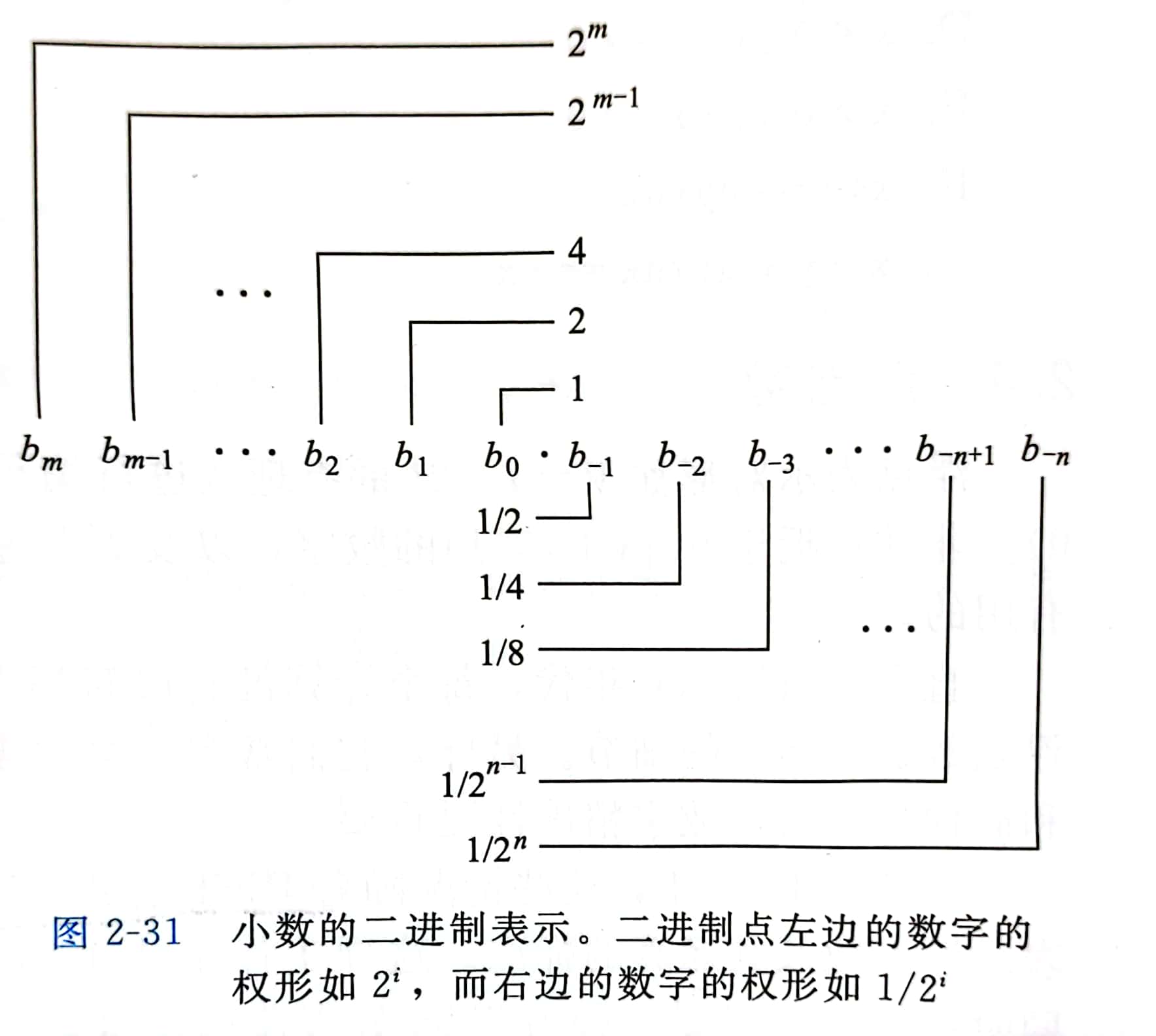
二进制小数
IEEE浮点表示
$V =(-1)^s \times M \times 2^E$
- 符号 s决定这个数的正负,而对于数值0的符号位解释作为特殊情况处理
- 尾数 M是一个二进制小数,它的范围是
1 ~ 2-ε或是0 ~ 1-ε - 阶码 E的作用是对浮点数加权,这个权重是 2 的 E 次幂 (可能是负数),用于存储科学计数法中的指数数据,并且采用移位存储。float类型的阶码是 8 位,double类型的阶码是 11 位
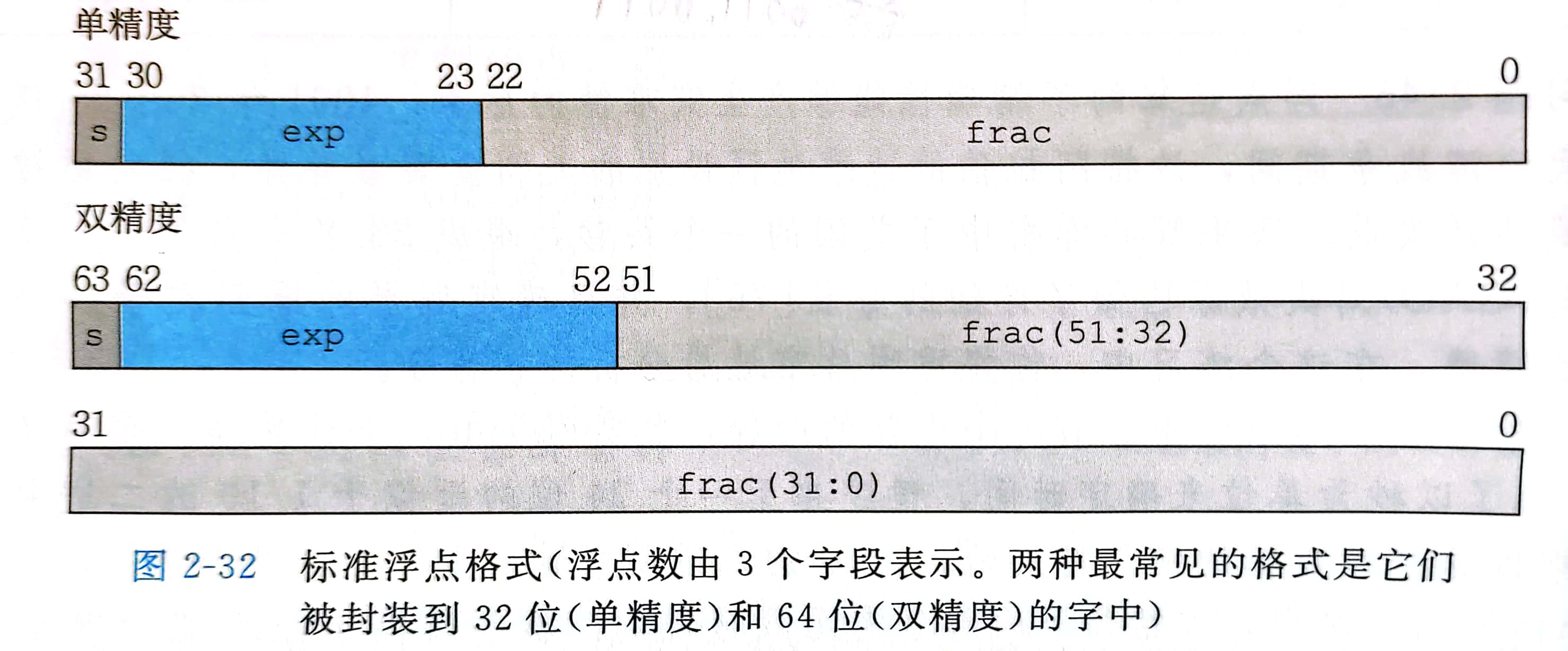
将浮点数表示的位划分成三个字段:
符号位+指数位偏移+尾数位

- 一个单独的符号位 s,直接编码符号 s
- k位的阶码字段 (exponent) 编码阶码E
- n位的小数字段 (frac) 编码尾数M,但编码出来的值也依赖于阶码字段的值是否等于0
单精度浮点数 float 中,s、exp和frac字段分别为 1 位、k = 8 位和 n = 23 位,得到32位的表示
双精度浮点数 double 中,s、exp和frac字段分别为 1 位、k = 11 位和 n = 52 位,得到64位的表示
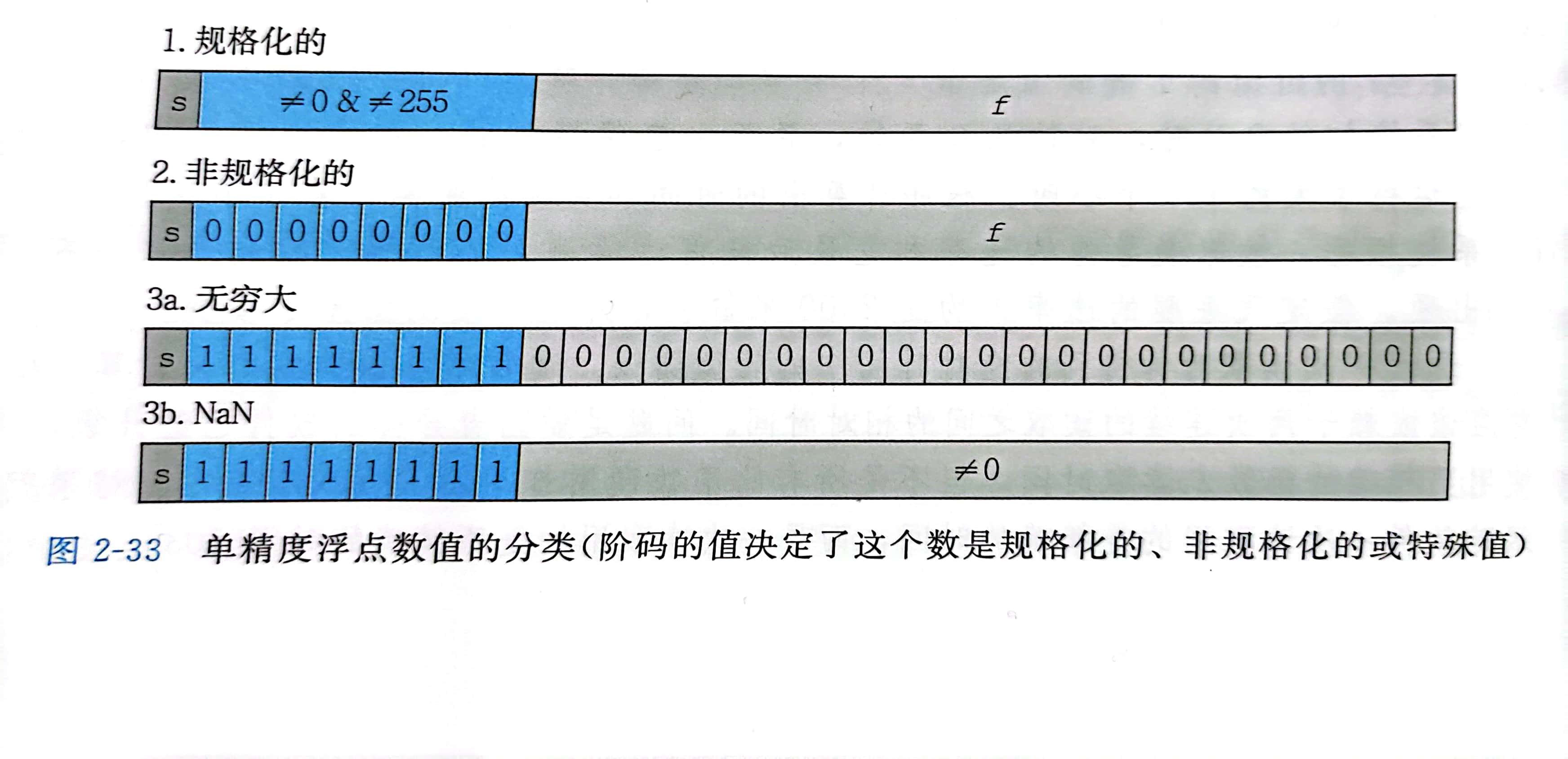
规格化的值
当阶码的位模式既不全为 0 (数值0),也不全为 1 (255或2047) 时,
阶码字段被解释为以 偏置 (Bias) 形式表示的有符号整数
即 阶码的值是 E = e - Bias,其中 e 是无符号数,而 Bias 等于 2^(k-1) - 1
由此产生的指数的取值范围,对于单精度是 -126 ~ +127,对于双精度是 -1032 ~ +1023
小数字段 frac 被解释为描述小数值 f,其中 0 <= f < 1,以二进制小数的形式表示 (二进制小数点在frac字段的最高有效位的左边)
尾数定义为 M = 1 + f
这种方法也叫做 隐含的以 1 开头的 表示
非规格化的值
当阶码域为全 0 时,所表示的数是 非规格化 形式
阶码值是 E = 1 - Bias,尾数值是 M = f,也就是小数字段的值,不包含隐含的开头的1
用途:
- 提供了一种表示数值 0 的方法
- 表示非常接近于 0.0 的数,提供了一种属性,称为
逐渐下溢
特殊值
当阶码全为 1 时:
- 小数域全为 0 时,得到值是无穷 s = 0 +∞ , s = 1 -∞
- 小数域非零时,结果为
NaN
 对P82举例的注释:
由公式 V = (-1)^s * M * 2^E
因为 12345 = 1.1000000111001 * 2^13,小数表示,将小数点前的1丢弃
所以 E = 13
对于float,frac部分有 23位,exp部分有 8位,符号位 1位
frac: 在1000000111001 (13位) 后增加 10 个 '0'
exp: 因为float的偏置量为
对P82举例的注释:
由公式 V = (-1)^s * M * 2^E
因为 12345 = 1.1000000111001 * 2^13,小数表示,将小数点前的1丢弃
所以 E = 13
对于float,frac部分有 23位,exp部分有 8位,符号位 1位
frac: 在1000000111001 (13位) 后增加 10 个 '0'
exp: 因为float的偏置量为 2^(8-1) - 1 = 127,我们的E已经是转换之后的,所以E需要加上偏置量127,得到140,二进制表示为 10001100
s: 正数 0
得到IEEE单精度表示 0100110010000001110010000000000
对于2.49的注释 n + 1 位二进制的小数是 n 位,因此2 (n + 1) + 1 位不能表示
舍入
因为表示方法限制了浮点数的范围和精度,所以浮点运算只能近似的表示实数运算 因此采用一种系统的方法,可以找到最接近的匹配值,它可以用期望的浮点形式表示出来,这就是舍入运算完成的任务
IEEE浮点格式定义了四种不同的舍入方式
向偶数舍入,也成向最接近的值舍入,是默认方式
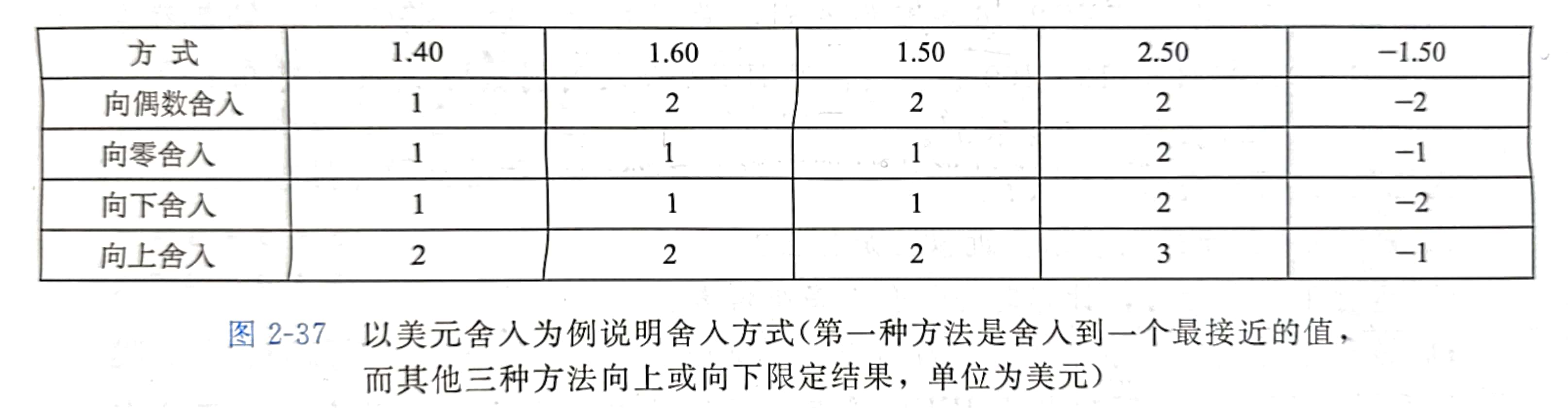
向偶数舍入的原因: 计算一组数据的平均值,向上或向下舍入会使平均数比真实值略高或略低 向偶数舍入在大多数情况下避免了这种统计误差,向上和向下舍入各有50%的可能 一般来说,只有对形如 XX...YXYYXXX.YXXYY100... 的二进制位模式的数,这种舍入方式才有效 最右边的Y的是要被舍入的位置
例: 10.00011 向下舍入到 10.00 10.00110 向上舍入到 10.01 10.10100 向下舍入到 10.10,因为这个值是两个可能值的中间值,并且我们倾向于使最低有效位为0
浮点运算
把浮点值 x 和 y 看成是书,而某个运算X定义在实数上,计算将产生 Round(x X y),这是队实际运算的精确结果进行舍入的结果 浮点加法不具有结合性,这是缺少的最重要的群属性 因此编译器倾向于保守,避免任何对功能产生影响的优化

