KMP 算法
简介
Knuth-Morris-Pratt字符串查找算法(简称为KMP算法)可在一个字符串S内查找一个词W的出现位置。一个词在不匹配时本身就包含足够的信息来确定下一个匹配可能的开始位置,此算法利用这一特性以避免重新检查先前配对的字符。——引自维基
在模式匹配问题中,KMP算法比Manacher算法更具普适性,Manacher算法只适用于 回文串 问题,较为局限。
例题引入
以 LeetCode 28. 找出字符串中第一个匹配项的下标 为例
题目给出一个字符串 text 和一个模式串 pattern,要求返回 text 中第一次匹配模式串的下标
例:text = ababc, pattern = abc, answer = 2
暴力解法
public static int strStr(String text, String pattern) {
int textLen = text.length();
int patternLen = pattern.length();
for (int i = 0; i < textLen - patternLen; i++) {
boolean flag = true;
for (int j = 0; j < patternLen; j++) {
if (pattern.charAt(j) != text.charAt(i + j)) {
flag = false;
break;
}
}
if (flag) {
return i;
}
}
return -1;
}
很容易看出时间复杂度为 O(m * n)
 原因是每次内循环匹配失败后,j 总是回溯到0,重新匹配
而
原因是每次内循环匹配失败后,j 总是回溯到0,重新匹配
而匹配失败的意思是当前字符不匹配,而当前字符之前的子串是匹配的
而KMP算法就是利用了这一特性,使得复杂度降低到了 O(m + n)
KMP算法
最长公共前后缀
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串
例如:
aabaa 的前缀是 aaba 后缀是 abaa
而 公共 则要求前后缀相等
则 aabaa 的最长公共前后缀是 aa
next数组
我们用 i 表示字符串的结尾,j 表示该字符串前缀的结尾
构造next数组的过程其实是 pattern自我匹配 的过程
pattern = aabaaf
"a" 无意义,不满足前后缀定义,i 从 1 开始
"aa" i = 1, j = 1, next[1] = 1
"aab" i = 2, j = 0, next[2] = 0
"aaba" i = 3, j = 1, next[3] = 1
"aabaa" i = 4, j = 2, next[4] = 2
"aabaaf" i = 5, j = 0, next[5] = 0
代码实现
int patternLen = pattern.length();
int[] next = new int[patternLen];
// 构造next[]
// i 指向 子串的最后
// j 指向 前缀的最后
for (int i = 1, j = 0; i < patternLen; i++) {
// 不匹配, j 为 长度-1 子串的结果
while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if (pattern.charAt(i) == pattern.charAt(j)) {
j++;
}
// 长度为 i 的子串的最长公共前后缀的长度为 j, 索引为 j - 1
// 即存放公共前后缀之后的字符的索引
next[i] = j;
}
匹配搜索
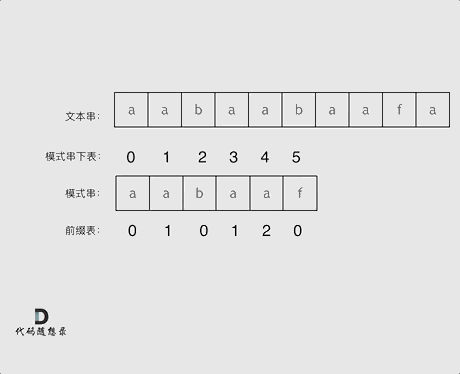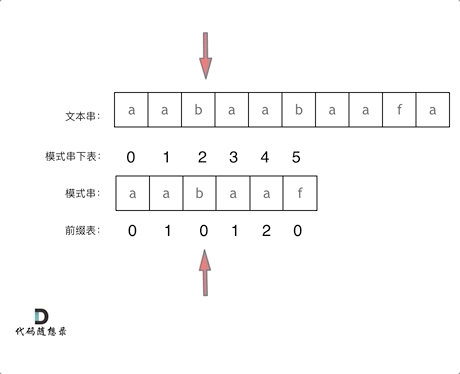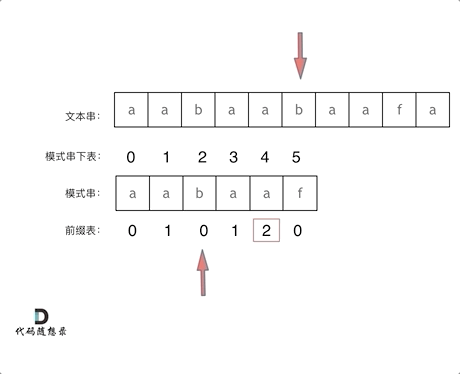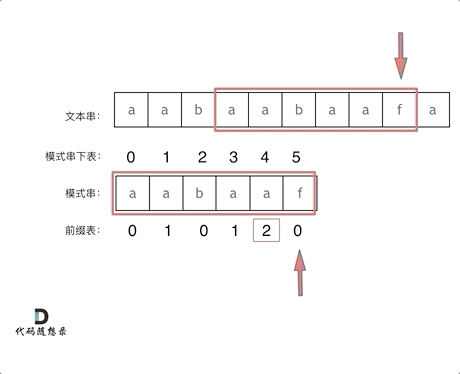
int textLen = text.length();
// search
// i 指向 text
// j 指向 pattern
for (int i = 0, j = 0; i < textLen; i++) {
// 不匹配, j 为 长度-1 子串的结果,
// 直到匹配, 边界情况为 j = 0
while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
// 匹配, j 后移
// 除前面全不匹配外,均匹配
if (text.charAt(i) == pattern.charAt(j)) {
j++;
}
if (j == patternLen) {
return i - patternLen + 1;
}
}
实现
public static int kmp(String text, String pattern) {
int textLen = text.length();
int patternLen = pattern.length();
int[] next = new int[patternLen];
// 构造next[]
// i 指向 子串的最后
// j 指向 前缀的最后
for (int i = 1, j = 0; i < patternLen; i++) {
// 不匹配, j 为 长度-1 子串的结果
while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if (pattern.charAt(i) == pattern.charAt(j)) {
j++;
}
// 长度为 i 的子串的最长公共前后缀的长度为 j, 索引为 j - 1
// 即存放公共前后缀之后的字符的索引
next[i] = j;
}
// search
// i 指向 text
// j 指向 pattern
for (int i = 0, j = 0; i < textLen; i++) {
// 不匹配, j 为 长度-1 子串的结果,
// 直到匹配, 边界情况为 j = 0
while (j > 0 && text.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
// 匹配, j 后移
// 除前面全不匹配外,均匹配
if (text.charAt(i) == pattern.charAt(j)) {
j++;
}
if (j == patternLen) {
return i - patternLen + 1;
}
}
return -1;
}
参考资料:
1.KMP 算法详解
2.代码随想录
3.【喵的算法课】KMP算法 av808837277
4.【宫水三叶】简单题学 KMP 算法
5.海纳的知乎回答
6.Wiki

